9514 1404 393
Answer:
- domain: x ∉ {-4, 3}
- range: y ∉ {1}
- horizontal asymptote: y=1
- vertical asymptote: x=3
Explanation:
The expression reduces to ...
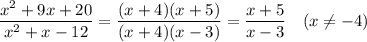
The domain is limited to values of x where the expression is defined. It is undefined where the denominator is zero, at x=-4 and x=3. The graph of the expression has a "hole" at x=4, where the numerator and denominator factors cancel.
- the domain is all real numbers except -4 and +3
The function approaches the value of 1 as x gets large in magnitude, but it cannot take on the value of 1.
- the range is all real numbers except 1
As discussed in 'range', there is a horizontal asymptote at y=1. That is the value you would get if you were to determine the quotient of the division:*
(x+5)/(x-3) = 1 + (8/(x-3)) . . . . quotient is 1
There is a vertical asymptote at the place where the denominator is zero in the simplified expression: x = 3.
- vertical asymptote at x=3; horizontal asymptote at y=1
_____
* For some rational functions, the numerator has a higher degree than the denominator. In those cases, the quotient may be some function of x. The "end behavior" of the expression will match that function. (Sometimes it is a "slant asymptote", sometimes a higher-degree polynomial.)