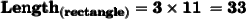Given :
- The length of a rectangle is thrice it's breadth.
- The perimeter of the rectangle is 88.
⠀
To Find :
The Length and breadth of the rectangle.
⠀
Solution :
We know that,
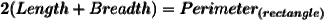
⠀
Let's assume the breadth of the rectangle as x cm. Then the length will become 3x.
⠀
Now, Substituting the given values in the formula :
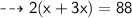
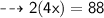
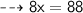
Dividing 8 by both sides :
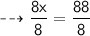
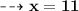
⠀
Therefore,