Question

a rock is thrown horizontally from the top of a cliff at 12 meters per second . calculate the time required for the rock to fall 45 meter vertically

Answer 1

Approximately 3.03 seconds.

Step-by-step explanation:

The distance traveled in the vertical direction is given by the kinematic equation:

`\displaystyle y = v_(iy)t + (1)/(2)at^2`

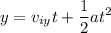
Where v_iy and a are the initial velocity and acceleration of the object, respectively, in the vertical direction.

Because the rock is thrown horizontally, there is no horizontal velocity. Therefore:

`\displaystyle y = (1)/(2) at^2`

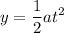
The vertical acceleration is simply gravity g. This, this yields the general equation:

`\displaystyle y = (1)/(2)gt^2`

Substitute 45 m for y and solve for time t:

`\displaystyle \begin{aligned} (45\text{ m}) & = (1)/(2)(9.8\text{ m/s$^2$})t^2 \\ \\ t^2 & =(450)/(49)\text{ s$^2$} \\ \\ & \approx 3.03\text{ s}\end{aligned}`

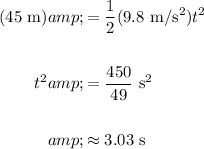
Therefore, it will take approximately 3.03 seconds for the rock to fall 45 meters vertically.