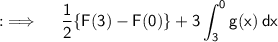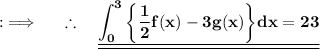Let's first write the given we have :
Now , let's assume that ;
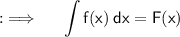
Now , proceeding further ;
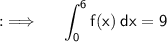
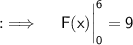
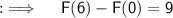
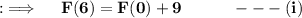
Also , we are given with ;
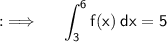
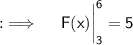
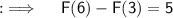
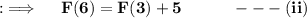
Now from (i) & (ii)
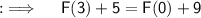

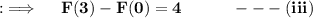
Now , let's go to what we have to find ;
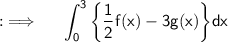
From the distributive of Integrals property we have ;
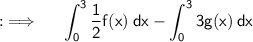
We knows that we can take out the Constant from the Integrand , So
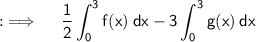
Now , we knows a property of definite Integrals :
Using this property and expanding the definite integral of f(x) we have ;