First take note of the domain of f(x) ; the square root term is defined as long as x - x ² ≥ 0, or 0 ≤ x ≤ 1.
Check the value of f(x) at these endpoints:
f (0) = 0
f (1) = 0
Take the derivative of f(x) :


For x ≠ 0, we can eliminate the √x term in the denominator:
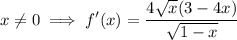
f(x) has critical points where f '(x) is zero or undefined. We know about the undefined case, which occurs at the boundary of the domain of f(x). Check where f '(x) = 0 :
√x (3 - 4x) = 0
√x = 0 or 3 - 4x = 0
The first case gives x = 0, which we ignore. The second leaves us with x = 3/4, at which point we get a maximum of max{f(x) } = 3√3 / 2.