Question

A ball with a weight of 70 N hangs from a string that is coiled around a 3 kg pulley with a radius of 0.4 m. Both the ball and the pulley are initially at rest. The rotational inertia of the pulley is 0.5mr2 and the ball is released from rest. Calculate the ball's velocity after it falls a distance of 2 meters.

Answer 1

v = 6.195 m / s

Step-by-step explanation:

For this exercise we can use the conservation of energy, for the system formed by the ball and the pulley

starting point. Higher before releasing the system

Em₀ = U = M g h

final point. When the ball has lowered h = 2

Em_f = K = ½ M v² + ½ I w²

the energy is preserved

Em₀ = Em_f

M g h = ½ M v² + ½ I w²

angular and linear velocity are related

v = w r

w = v / r

indicate that the moment of inertia is

I = ½ m r²

we substitute

M g h = ½ M v² + ½ (½ m r²) (v/r) ²

½ v² (M +
`(1)/(2)` m) = M g h

v² =
`2gh \ (M)/(M + (m)/(2) )`

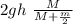
let's calculate

v =
`\sqrt{ 2 \ 9.8 \ 2 \ (70)/(70 + 1.5) }`

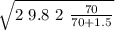
v = 6.195 m / s