Question

Jason stands on a cliff 24m above the ground and throws a ball upward at 16m/s determine the speed of the ball when it hits the ground below the cliff.

Answer 1

27 m/s

Step-by-step explanation:

Positive direction: up

v₀ = 16 m/s, y₀ = 24 m, g = -9.8 m/s², y = 0 (ground)

Use v² - v₀² = 2g(y - y₀)

v² - 16² = 2*(-9.8)*(0 - 24)

v² = 256 + 470.4 = 726.4

so v = 27 m/s

Answer 2

About 26.95 m/s.

Step-by-step explanation:

We can let downwards be the positive direction and upwards be the negative direction.

The ball is thrown upwards at a speed of 16 m/s. (Hence, the initial velocity is expressed as -16 m/s.)

Find the time it took for the ball to travel to its highest point. At this point, its velocity is zero. Find time t using a kinematic equation. In the vertical direction, the acceleration is gravity:

`\displaystyle \begin{aligned} v_y & = v_i + gt \\ \\ (0) & = (-16\text{ m/s}) + (9.8\text{ m/s$^2$})t \\ \\ t &= (80)/(49) \text{ s}\end{aligned}`

Find the distance it traveled during this time by using the following kinematic equation:

`\displaystyle \begin{aligned} y & = v_(i)t + (1)/(2)gt^2 \\ \\ & = (-16\text{ m/s})\left((80)/(49)\text{ s}\right) + (1)/(2)(9.8\text{ m/s$^2$})\left((80)/(49)\text{ s}\right)^2 \\ \\ & \approx -13.0612 \text{ m}\end{aligned}`

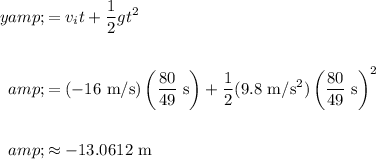
Hence, the ball traveled a total of 13.0612 meters when thrown into the air.

Thus, its total height is:

`\displaystyle h_\text{max} = 24 \text{ m} + 13.0612 \text{ m} = 37.0612\text{ m}`

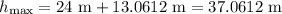
At this point, it will fall back down with an initial velocity of zero.

Find the time it took for the ball to hit the ground below the cliff:

`\displaystyle \begin{aligned} y & = v_(i)t + (1)/(2)gt^2 \\ \\ (37.0612\text{ m}) & = (0\text{ m/s})t + (1)/(2)(9.8\text{ m/s$^2$})t^2 \\ \\ t & \approx 2.75\text{ s} \end{aligned}`

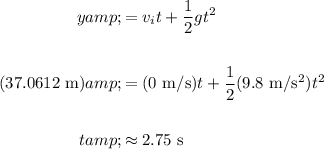
Find its final velocity using a kinematic equation:

`\displaystyle \begin{aligned} v_(f) & = v_(i) + gt \\ \\ & = (0\text{ m/s}) + (9.8\text{ m/s$^2$})(2.75\text{ s}) \\ \\ & = 26.95\text{ m/s}\end{aligned}`

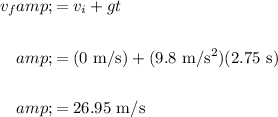
In conclusion, the final velocity of the ball is about 26.95 m/s.