Question

Figure 3.50 shows a wooden cube floating in water.

When a stone is placed on the wood, it sinks a further 0.2m.
Find the weight of the
(a) wood
(b) stone
(Density of water = 1000kgm^-3]​

Answer 1

(a) The weight of the wood is approximately 5,886 N

(b) The weight of the stone is approximately 1,962 N

Step-by-step explanation:

The given parameters are;

The base area of the wood, A = 1 m × 1 m = 1 m²

The depth to which the wood is submerged below the water, d = 0.6 m

The depth further the wood sinks when a stone is placed on the wood, Δd = 0.2 m

The density of water, ρ = 1,000 kg/m³

(a) Archimedes' principle states that the up-thrust, or upward force acting on an object submerged in a fluid, is equal to the weight of the displaced fluid.

For a floating object such as the wood, the up-thrust is equal to the weight of the object

The weight of the water displaced, W = The volume of the displaced water, V × The density of the water, ρ × The acceleration due to gravity, g

W = V × ρ × g

'V' is the same as the volume of the submerged wood, therefore;

V = A × d = 1 m × 1 m × 0.6 m = 0.6 m³

g ≈ 9.81 m/s²

Therefore;

W = 0.6 m³ × 1,000 kg/m³ × 9.81 m/s² ≈ 5,886 Newtons

The weight of the water displaced, W ≈ 5,886 N = The up-thrust = The weight of the wood

∴ The weight of the wood, W ≈ 5,886 N

(b) Similarly, the weight of the stone,
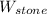`W_(stone)` is equal to the weight of the additional volume of water displaced

∴
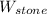`W_(stone)` = A × Δd × ρ × g

By plugging in the values, we get

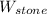`W_(stone)` ≈ 1 m² × 0.2 m × 1,000 kg/m³ × 9.81 m/s² = 1,962 N

The weight of the stone,
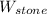`W_(stone)` ≈ 1,962 Newtons