Question

An element with mass 800 grams decays by 8.2% per day. How much of the element is remaining after 15 days,

to the nearest 10th of a gram?

Answer 1

Given:

The initial mass of an element is 800 grams.

Decay rate = 8.2% per day

Number of days = 15

To find:

The remaining element after 15 days.

Solution:

The exponential decay model is

`y=a(1-r)^t`

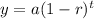
Where, a is the initial value r is the rate of interest and t is time period.

Putting
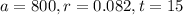`a=800,r=0.082,t=15` in the above formula, we get

`y=800(1-0.082)^(15)`

`y=800(0.918)^(15)`

`y=221.68188`

`y\approx 221.7`

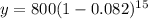
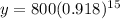
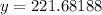
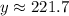
Therefore, the mass of the remaining element is 221.7 grams.