Answer:
0.0793 > 0.01, which means that we have a result in line with the manufacturer's claim.
Explanation:
Manufacturer’s claim that the average nicotine content does not exceed 3.5 mg
This means that the null hypothesis is given by:
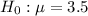
And the alternate hypothesis is:

The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
3.5 is tested at the null hypothesis
This means that
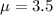
A random sample of 8 cigarettes of a certain brand has an average nicotine content of 4.2 milligrams and a standard deviation of 1.4 milligrams.
This means that
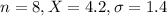
Value of the z-statistic:

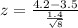
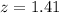
Pvalue of the test:
We are testing if the mean is higher than 3.5.
The sample mean found is of 4.2, and we have to find the probability of finding a sample mean at least as large as this, which is 1 subtracted by the pvalue of z = 1.41.
z = 1.41 has a pvalue of 0.9207
1 - 0.9207 = 0.0793
0.0793 > 0.01, which means that we have a result in line with the manufacturer's claim.