Answer:
The error are
1) The use of the angle addition postulate, for
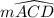
2) The assumption that
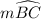 = 90°
= 90°
The vertical angle property between
 and
and
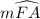 should be used to find 'x'
should be used to find 'x'
x = 5
Explanation:
From the drawing of the circle, we are given;
AD = A diameter of the circle
∴
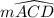 = 180°
= 180°
By angle addition postulate, we have;
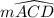 =
=
 +
+
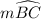 +
+

By substitution property of equality, we have;
180° =
 +
+
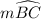 +
+

 = 5·x°
= 5·x°
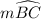 = Not given
= Not given
 = 15·x°
= 15·x°
However;
 is the vertically opposite angle to
is the vertically opposite angle to
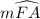
∴
 =
=
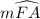 = (16·x - 5)°
= (16·x - 5)°
 = 15·x° = (16·x - 5)°
= 15·x° = (16·x - 5)°
15·x° = (16·x - 5)°
∴ 5 = 16·x° - 15·x° = x
x = 5
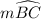 = 180° - (
= 180° - (
 +
+
 ) = 180° - (15·x° + 5·x°) = 180° - (20·x°)
) = 180° - (15·x° + 5·x°) = 180° - (20·x°)
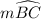 = 180 - (20×5)° = 80°
= 180 - (20×5)° = 80°
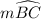 = 80°
= 80°
The error are the use of the angle addition postulate, for
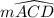 , and the assumption that
, and the assumption that
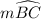 = 90° rather than the vertical angle property between
= 90° rather than the vertical angle property between
 and
and
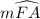 in trying to find 'x', from which x = 5.
in trying to find 'x', from which x = 5.