Given:
The equation is:
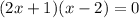
To find:
The values of a, b and b from the standard form.
Solution:
The standard form of a quadratic equation is:
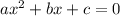 ....(i)
....(i)
We have,
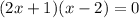
In can be rewritten as
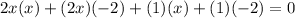
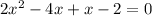
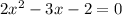 ...(ii)
...(ii)
On comparing (i) and (ii), we get
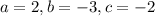
Therefore, the correct option is C.