Question

Triangle CDE, with vertices C(-8,-7), D(-2,-8) and E(-5,-2), is drawn on the coordinate grid below.

What is the area, in square units, of triangle CDE?

Answer 1

Area = 24.75 sqr units

Explanation:

You will need these formulas:

`d = √((x_2 - x_1)^2 + (y_2-y_1)^2)`

Midpoint =
`((x_(1) + y_(1) )/(2) , (x_(2) + y_(2) )/(2))`

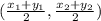
Area = b x h

Let us treat CD as the base. Find the length of the base with the distance formula. Use the coordinates for points C & D.

`d = √((-2 - (-8))^2 + (-8-(-7))^2)`

`d = √(37)`

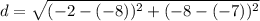
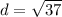
The base is
`√(37)`.

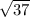The height is the distance between point E and the midpoint of line CD.

Midpoint of CD =
`((-8 + (-7) )/(2) , (-2 + (-8) )/(2))` = (
`-(15)/(2)`,
`-5`)

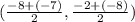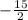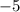Use the distance formula to find the height.

`d = \sqrt{(-5 - (-(15)/(2) ))^2 + (-2-(-5))^2}`

`d = (√(61) )/(2)`

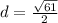
Find the area with the two distances that were found.

Area =
`(√(37)) ((√(61) )/(2))`

Area =
`(√(2257) )/(2)`

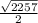
Area = 24.75 sqr units