Answer:
One Triangle = 2.09 in²
Two Triangles = 4.18 in²
Rectangle = 17.48 in²
Total area of whole trapezoid = 21.66 in²
Explanation:
Since it was not clarified which region is shaded we will just find the area of each individual part of the shape.
Let's start with the triangles.
1. To find the area of a triangle, the formula is
 . It is given that the base of one triangle is equal to 1.1 in and the height is equal to 3.8 in., so in the equation, it would look like:
. It is given that the base of one triangle is equal to 1.1 in and the height is equal to 3.8 in., so in the equation, it would look like:
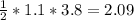 in²
in²
2. So now that we know one triangle is equal to 2.09 in², we now know that the other triangle is equal to the same area. To find the total of the two triangles you need to multiply the area by 2:
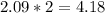 in²
in²
Moving on to the rectangle...
1. To find the area of the rectangle we need to use the formula base times height or b x h. It is given that the height is 3.8 in while the length is 4.6 in. So in the equation it would look like:
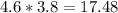 in²
in²
Now to find the total area of all shapes combined...
1. To do this, we just need to add up all the areas we found, so...
17.48 + 4.18 = 21.66 in²