Hello!
For this uniform distribution, the shape of the density function is a line. We can begin by identifying key elements of the distribution:
Range: 6 to 14 pounds
Formula of density function:
y = 1/Range
1 - (14 - 6) = 1/8 = 0.125
f(x) = 0.125
1)
P(x = 7)
A uniform distribution is a continuous distribution, so the probability of x being an EXACT value is approximately 0.
This is the same as if we took the following integral. (Finding the area under a curve with the same start and end point)
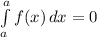
Therefore, P(x = 7) = 0.
2)
We can think of this as finding the area of a rectangle.
The width would be the difference between 8.25 pounds and 12 pounds:
W = 12 - 8.25 = 3.75
The height would be the function (y = .125), or:
h = .125
Using the equation for the area of a rectangle: (A = h * w)
A = 3.75 * .125 = 0.469
Thus, P(8.25 < x < 12) = 0.469
3)
To find the probability GREATER than 10.50 pounds, we can subtract this value from the max value for the width:
W = 14 - 10.50 = 3.50
The height is the same as above:
h = .125
Solve for the area:
A = 3.50 * .125 = 0.4375
P(x > 10.5) = 0.4375