Question:
A population consists 1, 2, 4, 5, 8. Draw all possible samples of size 2 without replacement from this population.
Verify that the sample mean is an unbiased estimate of the population mean.
Answer:

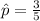 --- proportion of evens
--- proportion of evens
The sample mean is an unbiased estimate of the population mean.
Explanation:
Given
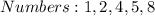
Solving (a): All possible samples of 2 (W.O.R)
W.O.R means without replacement
So, we have:

Solving (b): The sampling distribution of the proportion of even numbers
This is calculated as:
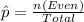
The even samples are:
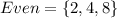
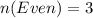
So, we have:
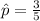
Solving (c): To verify

Calculate the mean of each samples

Calculate the mean of the sample means
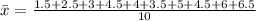
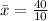
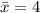
Calculate the population mean:
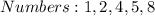
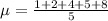

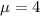
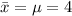
This implies that
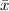 is an unbiased estimate of the
is an unbiased estimate of the
