Answer:
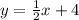
Explanation:
Slope intercept form is:
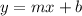
y and x remain as variables and don't get changed or touched.
m is the slope of the line.
b is the y-intercept of the line.
To find the information needed for this form, we need to use the equation:
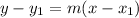
We are given that the slope is
 , so we plug it in for m:
, so we plug it in for m:
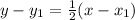
Now, we need to plug in the given value of
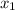 and
and
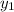 in the point (-6, 1), where the x = -6 and y = 1. So it will look like this when plugged into the equation:
in the point (-6, 1), where the x = -6 and y = 1. So it will look like this when plugged into the equation:
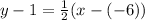
Solve for y (isolate y on one side):
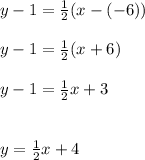
Final answer is: y = 1/2x + 4