Answer: k = 6+10x
=======================================================
Work Shown:
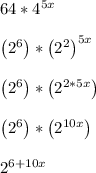
The result is in the form
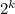 with k = 6+10x
with k = 6+10x
------------------------
Step-by-step explanation:
First we need to get everything as an exponential expression with a base 2.
We rewrite 64 as
 and 4 as
and 4 as
 in the second step.
in the second step.
In the third step, I used the rule
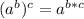 which says to multiply the exponents together. That's how I went from
which says to multiply the exponents together. That's how I went from
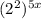 to
to
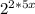 . Then the 2*5x in the exponent becomes 10x.
. Then the 2*5x in the exponent becomes 10x.
To wrap things up, I used the rule
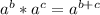 which says to add the exponents when we multiply stuff of the same base together.
which says to add the exponents when we multiply stuff of the same base together.