Answer:
Area of ΔQRS = 2.3 square inches
Explanation:
From the given information,
<S + <Q + <R =
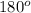
51 + 44 + <R =
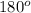
95 + <R =
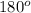
<R =
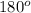 - 95
- 95
=
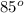
<R =
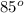
Applying the Sine rule, we have;
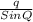 =
=
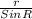 =
=
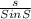
Using
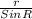 =
=
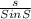
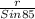 =
=
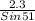
r =
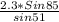
= 2.9483
r = 2.9 inches
Also,
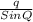 =
=
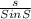
 =
=
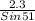
q =

= 2.0559
q = 2.0 inches
From Herons formula,
Area of a triangle =
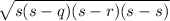
s =
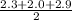
= 3.6
Area of ΔQRS =
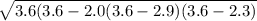
= 2.2895
Area of ΔQRS = 2.3 square inches