Hi, can someone please help, and possibly explain the answer please.

Question

asked Dec 21, 2022 187k views

1 Answer

Teboto · Answer 1 · 2022-12-25T19:32:42+0000

Answer:

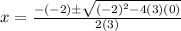
$x=(-(-2)\±√((-2)^2-4(3)(0)) )/(2(3))$

Explanation:

Quadratic formula:
$x=(-b\±√(b^2-4ac) )/(2a)$ when the equation is
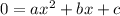
0=ax^2+bx+c

The given equation is
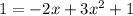1=-2x+3x^2+1 . Let's first arrange this so its format looks like
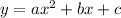y=ax^2+bx+c :

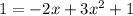
1=-2x+3x^2+1

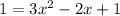
1=3x^2-2x+1

Subtract 1 from both sides of the equation

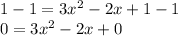
$1-1=3x^2-2x+1-1\\0=3x^2-2x+0$

Now, we can easily identify 3 as a, -2 as b and 0 as c. Plug these into the quadratic formula:

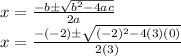
$x=(-b\±√(b^2-4ac) )/(2a)\\x=(-(-2)\±√((-2)^2-4(3)(0)) )/(2(3))$

I hope this helps!