25.
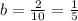
_____________________________________________
26 .
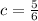
_____________________________________________
27 .
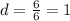
_____________________________________________
31 .
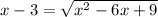
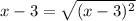
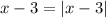
Thus :
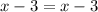
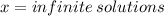
OR
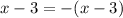
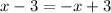
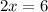
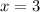
_____________________________________________
32.
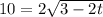
Divide both sides by 2
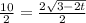
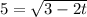
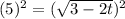
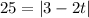
Switch sides
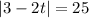
Thus :
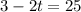
Subtract both sides 3
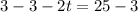
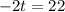
Divide both sides by -2
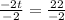
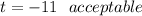
Or
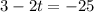
Subtract both sides 3
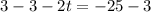
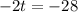
Divide both sides by -2
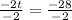
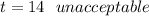
_____________________________________________
33.
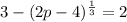
Subtract both sides 3
![3 - 3 - \sqrt[3]{2p - 4} = 2 - 3](https://img.qammunity.org/2023/formulas/mathematics/college/2wd9d07oyujvs5rll96ipyebrpumlpzp3r.png)
![- \sqrt[3]{2p - 4} = - 1](https://img.qammunity.org/2023/formulas/mathematics/college/20ujocmoll25e7yqj3x7wswtyfmibog4zj.png)
![\sqrt[3]{2p - 4} = 1](https://img.qammunity.org/2023/formulas/mathematics/college/x6k030o8myxnez8fqjf0rpru2atd8lwspz.png)
![({ \sqrt[3]{2p - 4} })^(3) = ({1})^(3)](https://img.qammunity.org/2023/formulas/mathematics/college/t9r6p7kleaup401b4wpm46h4c6rih7ca4a.png)
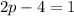
Add both sides 4
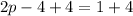
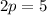
Divide both sides by 2
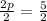
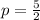
_____________________________________________
34.
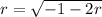
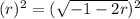
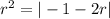
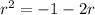
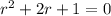
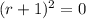
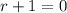
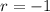
_____________________________________________
35.
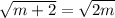
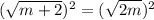
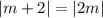
Thus :
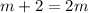
Switch sides
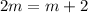
Subtract both sides m
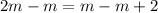
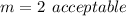
Or
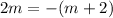
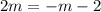
Add both sides m
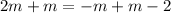
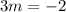
Divide both sides by 3
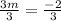
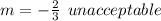
_____________________________________________
36 .
![\sqrt[3]{4x + 1} - \sqrt[3]{6x - 9} = 0](https://img.qammunity.org/2023/formulas/mathematics/college/pf1nd6nq4t65bnkmla37sgw0574525wzfr.png)
![\sqrt[3]{4x + 1} = \sqrt[3]{6x - 9}](https://img.qammunity.org/2023/formulas/mathematics/college/l2qrbgw9xiw527v1x7pnxpme26b5mmjfw5.png)
![({ \sqrt[3]{4x + 1} })^(3) = ({ \sqrt[3]{6x - 9} })^(3)](https://img.qammunity.org/2023/formulas/mathematics/college/ycmfd0kgvh29oh01fbu719rq09trg973j3.png)
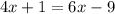
Switch sides
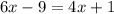
Subtract both sides 4x
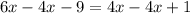
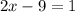
Add both sides 9
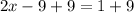
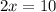
Divide both sides by 2
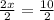
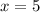
_____________________________________________
The last one is yours bro you got this ....
Have a great time ♡♡