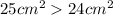Question

On the left, prism A. Prism A is a triangular prism. The base has side lengths of 6 centimeters, 8 centimeters, and 10 centimeters. On the right, prism B. Prism B is a rectangular prism. The base has side lengths of 5 centimeters and 5 centimeters.

Answer 1

Prism B has a larger base area

Explanation:

Given

Base dimensions:

Prism A:

Lengths: 6cm, 8cm and 10cm

Prism B:

Lengths: 5cm and 5cm

Required [Missing from the question]

Which prism has a larger base area

For prism A

First, we check if the base dimension form a right-angled triangle using Pythagoras theorem.

The longest side is the hypotenuse; So:

`10^2 = 8^2 + 6^2`

`100 = 64 + 36`

`100 = 100`

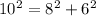
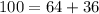
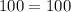
The above shows that the base dimension forms a right-angled triangle.

The base area is then calculated by;

Area = 0.5 * Products of two sides (other than the hypotenuse)

`Area = 0.5 * 8cm * 6cm`

`Area = 24cm^2`

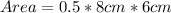
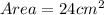
For Prism B

`Lengths = 5cm\ and\ 5cm`

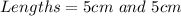
So, the area is:

`Area = 5cm * 5cm`

`Area = 25cm^2`

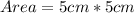
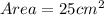
By comparison, prism B has a larger base area because
`25cm^2 > 24cm^2`