Question

2. A wooded area is in the shape of a a trapezoid whose bases measure 128 m and $2 m and its height is 40 m. A 4 m wide walkway is constructed which runs perpendicular from the two bases. Calculate the area of the wooded area after the addition of the watkway

Answer 1

Correction in the Question:

A wooded area is in the shape of a a trapezoid whose bases measure 128 m and 92 m and its height is 40 m. A 4 m wide walkway is constructed which runs perpendicular from the two bases. Calculate the area of the wooded area after the addition of the walkway.

Answer:

The wooded area after the addition of the walkway is 4240
`m^2`.

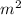Explanation:

we are given

length of the two bases = 128m and 92m

height of the trapezoid = 40m

the approximate figure of the given trapezoid is given as:

__ __ __ 92 __ __ _

/ | | | \

/ | 40 |4| \

/__ _| __ __ | |__ __ __ __ \

128

Area of a trapezoid = [(a + b)/2] * height, where a and b are representing the bases of the given trapezoid.

Area = [(92 + 128)/2] * 40

= [220/2] * 40

= 110 * 40

= 4400
`m^2`

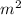
Now there is a 4m wide walkway is to be constructed in that trapezoid. The pathway will be a rectangle as it has 4m width and 40m height as it is perpendicular to both the bases.

Area of a rectangle = length * width

Area = 40 * 4

= 160

Since the walkway will reduce the area of the trapezoid as it is constructed upon it therefore the wooded area after the addition of the walkway is

4400 + (-160) = 4240
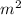`m^2`.