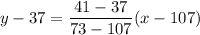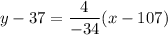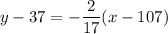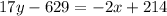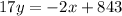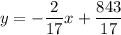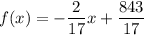Answer:
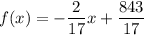
Explanation:
Given:
Score of 37 with 107 minutes on social media.
Score of 41 with 73 minutes on social media.
The two pieces of information above can be thought of as two points on a line. Since the quiz score is a function of the number of minutes on social medial, let the number of minutes on social media be x and the score be y. The given information gives us two ordered pairs: (107, 37) and (73, 41).
Now we need to write the equation of a line that passes through these two points.
The two-point form of the equation of a line is:
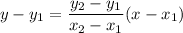
We have
 ,
,
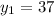 ,
,
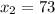 , and
, and
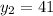 .
.