Question

If it is known that a motor battery has an input voltage of 12V and a capacity of 6 Ah, how much power and resistor value is required to turn on 8 lamps with a parallel circuit, with the specifications of each lamp having a maximum voltage of 3V and an electric current of 140 mA? How long did all the lights go on until they off?

Answer 1

Part A

The power to turn on the lamp, ∑P = 3.36 W

Part B

The Resistor required is approximately 8.04 Ohms

Part C

The time for all the lights to go out is approximately 21.43 hours

Step-by-step explanation:

The input voltage of the motor battery , V = 12 V

The capacity of the battery, Q = 6 Ah

The number of lamps in parallel = 8 lamps

The maximum voltage of each lamp, = 3 V

The electric current in each lamp = 140 mA

The energy available in a battery, E = Q × V

For the battery, we have;

E = 6 Ah × 12 V = 72 Wh

The energy available in a battery, E = 72 Wh

Part A

The power used by the lamps,
`P_i` =
`I_i` ×
`V_i`

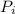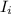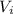
∴ The total power used by the lamp, ∑P = 8 × 0.14 A × 3 V = 3.36 W

The power to turn on the lamp, ∑P = 3.36 W

Part B

The resistance required, is given as follows;

Resistor required = (Battery voltage - Lamp voltage)/(The sum of bulb current)

∴ Resistor required = (12 V - 3 V)/(8 × 0.14 A)

The Resistor required = 8.03571429 Ohms

The Resistor required ≈ 8.04 Ohms

Part C

The time for all the lights to go out = The time for the lamps to use all the power available in the battery

The time for all the lights to go out, t = E/∑P

∴ t = 72 Wh/(3.36 W) = 21.4285714 h

∴ The time for all the lights to go out, t ≈ 21.43 h

The time for all the lights to go out = The time for the lamps to use all the power available in the battery = t ≈ 21.43 h

∴ The time for all the lights to go out ≈ 21.43 hours.