Answer:
a) 49 oz and 59 oz
b) 81.8 %
c) 99.9 %
Explanation:
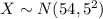
The Empirical Rule states that:
- 68% of the data falls within one standard deviation from the mean
- 95% of the data falls within two standard deviations from the mean
- 99.7% of the data falls within three standard deviations from the mean
a)
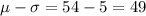
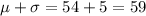
⇒ 68% of the widget weights lie between 49 oz and 59 oz
b) 59 oz is 1 standard deviation from the mean
44 oz is 2 standard deviations from the mean
Therefore, 84.1 - 2.3 = 81.8 %
c) 39 is 3 standard deviations from the mean
Therefore, 100 - 0.1 = 99.9 %
**Please find attached a sketch of the distribution. The mean is shown with the solid line and the standard deviations with dash lines**