Question

Help! What does the bracket mean and how do I do the questions?

Answer 1

maybe it meane 11/a

Explanation:

Answer 2

The bracket is the binomial.

The definition is:
`\binom{n}{k} = (n!)/(k!\cdot (n-k)!)`

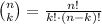
Note that
`\binom{n}{k} = \binom{n}{n-k}`

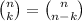
The meaning is "if we have n elements, how many ways are there to choose k of them?" From this definition it should be obvious that
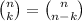`\binom{n}{k} = \binom{n}{n-k}` - if you're picking k, it's just as many ways as choosing the (n-k) that you're not picking.

The coefficient can be found by realizing that to get x^9, we need to choose (from the full multiplication):

• 9 brackets to provide x
• 2 brackets to provide the number 3

There's
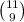`\binom{11}{9}` ways to do that, so the component for x^9 will be:

`\binom{11}{9} \cdot 3^2 \cdot x^9 = (11!)/(2!\cdot 9!) \cdot 3^2 \cdot x^9 = (10\cdot 11)/(2) \cdot 3^2 \cdot x^9 = 55 \cdot 9 \cdot x^9 = 495x^9`

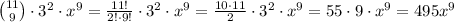
So:

a = 2

Coefficient is 495