Answer:
The angle above the horizontal at which the pitcher throws the ball determines the distance the ball travels before returning to the height at which it was thrown
Step-by-step explanation:
The baseball is thrown as a projectile and the range, 'R', of the baseball which is the distance the baseball travels before the height above the ground returns to the initial height is given given as follows;
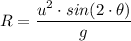
Where;
R = The range of the baseball = The horizontal distance away from the pitcher the ball reaches
u = The initial velocity with which the baseball was thrown
θ = The angle above horizontal a baseball pitcher throws the ball
g = The acceleration due to gravity ≈ 9.81 m/s²
From the the equation, when θ = 0, sin(θ) = sin(0) = 0 and the ball does not cover any horizontal distance before going lower than the height at which it was thrown, therefore, for the ball to travel further, the angle of launch, θ has to be larger than 0.