Question

Please help me with the question please ASAP

Answer 1

The ratio of perimeter of ABCD to perimeter of WXYZ =
`(2)/(3)`

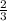
Explanation:

First, we have to determine the multiplicative factor of the dimensions for both figures.

Considering sides AB and WX,

multiplicative factor =
`(12)/(8)`

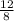
= 1.5

So that:

XY = 6 x 1.5 = 9

YZ = 7 x 1.5 = 10.5

ZW = 7 x 1.5 = 10.5

Perimeter of ABCD = 6 + 7 + 7 + 8

= 28

Perimeter of WXYZ = 9 + 10.5 + 10.5 + 12

= 42

The ratio of the perimeters of the two quadrilaterals can be determined as;

ratio =
`(perimeter of ABCD)/(Perirmeter of WXYZ)`

=
`(28)/(42)`

=
`(2)/(3)`

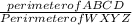
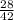
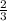
The ratio of the perimeter of ABCD to perimeter of WXYZ is
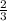`(2)/(3)`.