Given:
The figure of rectangle.
To find:
a. The diagonal of the rectangle.
b. The area of the rectangle.
c. perimeter of the rectangle.
Solution:
(a)
In a right angle triangle,

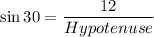
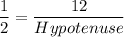

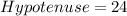
So, the diagonal of the of the rectangle is 24 units.
(b)
In a right angle triangle,
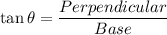
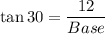
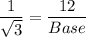
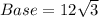
Length of the rectangle is 12 and width of the rectangle is
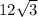 . So, the area of the rectangle is:
. So, the area of the rectangle is:
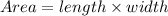
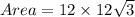
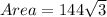
So, the area of the rectangle is
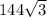 sq. units.
sq. units.
(c)
Perimeter of the rectangle is:
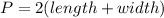
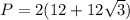
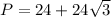
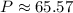
Therefore, the perimeter of the rectangle is about 65.57 units.