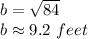Question

Find the length in feet of a leg of a right triangle whose hypotenuse is 10 feet and

other leg is 48 inches. Round to the nearest tenth of a foot.

Answer 1

9.2 feet

Explanation:

Start by converting the leg of the triangle to feet (note 1 foot = 12 inches):

`48\ inches((1\ foot)/(12\ inches))=4*1\ foot=4\ feet`

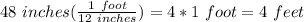
We can use the Pythagorean Theorem to find the length of the other leg...

`a^2+b^2=c^2`

Note that "a" and "b" represent the two legs of the triangle and "c" represents the length of the hypotenuse. We can substitute the given lengths into the equation to solve for the other leg.

`4^2+b^2=10^2\\16+b^2=100`

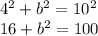
Subtract 16 from both sides:

`b^2=84`

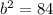
Take the square root of both sides:

`b=√(84)\\b\approx9.2\ feet`