Solution :
Given :
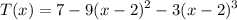
a). f(2) = T(2) = 7
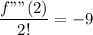 , so f''(2) =
, so f''(2) =
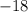
b). Yes, since f'(2) = T'(2)
 0,
0,
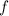 does have the critical point at
does have the critical point at
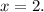
Since f''(2) =
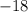 < 0,
< 0,
 is relative maximum value.
is relative maximum value.
c).

It is also not possible for determining if
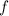 has a critical point at x = 0 because
has a critical point at x = 0 because
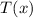 gives exact information only at
gives exact information only at
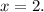
d). The Lagrange
 bound
bound
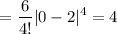
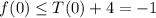
Therefore,
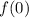 is negative.
is negative.