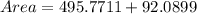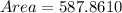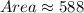Answer:
The area is approximately
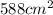
Explanation:
Given
See attachment for figure
Required
The area of the shaded region
The shaded region is as follows:
- A major segment
- A triangle
First, calculate the area of the major segment using:

Where
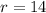

So, we have:
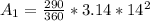
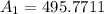
Next, the area of the triangle using:
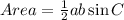
Where
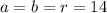
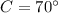
So, we have:

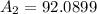
So, the area of the shaded region is: