Answer:
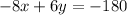
Explanation:
Given
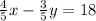
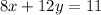
Required
Equivalent form of the first equation that eliminates x when added to the second
To do this, we simply make the coefficients of x to be opposite in both equations.
In the second equation, the coefficient of x is 8.
So, we need to make the coefficient of x -8, in the first equation.
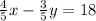
Multiply by -10
![-10 * [(4)/(5) x-(3)/(5)y=18]](https://img.qammunity.org/2022/formulas/mathematics/high-school/pnlor6y0ctpic9zi7yqi3cuygutdkspibe.png)
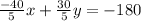
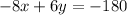
When this is added to the first equation, the x terms becomes eliminated