Question

Josie recorded the average monthly temperatures for two cities in the state where she lives. For City 1,

what is the mean of the average monthly temperatures? What is the mean absolute deviation of the
average monthly temperatures? Round your answers to the nearest tenth.
Average Monthly Temperatures for City 1 (°F)
45, 37, 64, 50, 44, 49, 73, 76, 27, 23, 49, 45
Average Monthly Temperatures for City 2 (°F)
30, 22, 49, 35, 29, 34,58,61, 12, 8, 34, 30
The mean average monthly temperature in City 1 is
OF.
The mean absolute deviation for the average monthly temperature in City 1 is
OF.

Answer 1

The mean average monthly temperature in City 1 is 48.75°F.

The mean absolute deviation for the average monthly temperature in City 1 is 13.375°F

Explanation:

For this case we have the following dataset given:

Average Monthly Temperatures for City 1 (° F)

30, 38, 66, 78, 47, 75, 35, 45, 56, 29, 49, 37

Average Monthly Temperatures for City 2 (° F)

15, 23, 51, 63, 32, 60, 20, 30, 41, 14, 34, 22

For this case the sample mean can be calculated with the following formula:

`$\bar{X}=(\sum_(i=1)^(n) x_(i))/(n)$`

And replacing we got:

`$\bar{X}_(1)=(30+38+66+78+47+75+35+45+56+29+49+37)/(12)=48.75$`

The mean average monthly temperature in City 1 is 48.75°F.

And now we can calculate the following values:

`$|38-48.75|=10.75$`

`$|66-48.75|=17.25$`

`$|78-48.75|=29.25$`

`$|47-48.75|=1.75$`

`$|75-48.75|=26.25$`

`$|35-48.75|=13.75$`

`$|45-48.75|=3.75$`

`$|56-48.75|=7.25$`

`$|29-48.75|=19.75$`

`$|49-48.75|=0.25$`

`$|37-48.75|=11.75$`

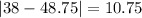
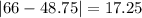
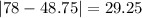
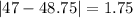
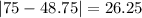
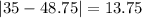
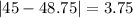
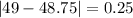
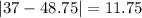
And the mean absolute deviation is given by:

`$M A D=\frac{\sum_(i=1)^(n)\left|X_(i)-\bar{X}\right|}{n}=(160.5)/(12)=13.375$`

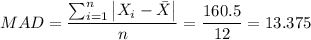
The mean absolute deviation for the average monthly temperature in City 1 is 13.375°F