Question

The volume of a gas decreases from 15.7 mºto 11.2 m3 while the pressure changes from 1.12 atm to 1.67 atm. If the

initial temperature is 245 K, what is the final temperature of the gas?
O 117 K
230 K
261K
.
O 512K

Answer 1

Approximately
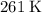`261\; \rm K`, if this gas is an ideal gas, and that the quantity of this gas stayed constant during these changes.

Step-by-step explanation:

Let
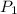`P_1` and
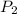`P_2` denote the pressure of this gas before and after the changes.

Let
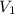`V_1` and
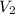`V_2` denote the volume of this gas before and after the changes.

Let
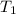`T_1` and
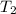`T_2` denote the temperature (in degrees Kelvins) of this gas before and after the changes.

Let
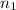`n_1` and
`n_2` denote the quantity (number of moles of gas particles) in this gas before and after the changes.

Assume that this gas is an ideal gas. By the ideal gas law, the ratios
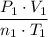`\displaystyle (P_1 \cdot V_1)/(n_1 \cdot T_1)` and
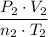`\displaystyle (P_2 \cdot V_2)/(n_2 \cdot T_2)` should both be equal to the ideal gas constant,
`R`.

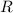In other words:

`R = \displaystyle (P_1 \cdot V_1)/(n_1 \cdot T_1)`.

`R =\displaystyle (P_2 \cdot V_2)/(n_2 \cdot T_2)`.

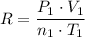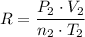Combine the two equations (equate the right-hand side) to obtain:

`\displaystyle (P_1 \cdot V_1)/(n_1 \cdot T_1) = (P_2 \cdot V_2)/(n_2 \cdot T_2)`.

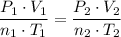Rearrange this equation for an expression for
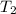`T_2`, the temperature of this gas after the changes:

`\displaystyle T_2 = (P_2)/(P_1) \cdot (V_2)/(V_1) \cdot (n_1)/(n_2) \cdot T_1`.

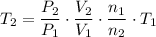Assume that the container of this gas was sealed, such that the quantity of this gas stayed the same during these changes. Hence:
`n_2 = n_1`,
`(n_2 / n_1) = 1`.

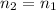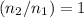`\begin{aligned} T_2 &= (P_2)/(P_1) \cdot (V_2)/(V_1) \cdot (n_1)/(n_2)\cdot T_1 \\[0.5em] &= (1.67\; \rm atm)/(1.12\; \rm atm) * (11.2\; \rm m^(3))/(15.7\; \rm m^(3)) * 1 * 245\; \rm K \\[0.5em] &\approx 261\; \rm K\end{aligned}`.