Answer:
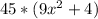
Explanation:
STEP
1
:
Equation at the end of step
1
:
((5x2•(34))+(5•(33)))+(5•32)
STEP
2
:
Equation at the end of step 2
((5x2•(34))+(5•(33)))+(5•32)
STEP
3
:
Equation at the end of step
3
:
((5x2 • (34)) + (5 • 33)) + (5•32)
STEP
4
:
Equation at the end of step 4
((5x2 • (34)) + (5•33)) + (5•32)
STEP
5
:
Equation at the end of step
5
:
((5x2 • 34) + (5•33)) + (5•32)
STEP
6
:
Equation at the end of step 6
((5•34x2) + (5•33)) + (5•32)
STEP
7
:
STEP
8
:
Pulling out like terms
8.1 Pull out like factors :
405x2 + 180 = 45 • (9x2 + 4)
Polynomial Roots Calculator :
8.2 Find roots (zeroes) of : F(x) = 9x2 + 4
Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0
Rational Roots Test is one of the above mentioned tools. It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers
The Rational Root Theorem states that if a polynomial zeroes for a rational number P/Q then P is a factor of the Trailing Constant and Q is a factor of the Leading Coefficient
In this case, the Leading Coefficient is 9 and the Trailing Constant is 4.
The factor(s) are:
of the Leading Coefficient : 1,3 ,9
of the Trailing Constant : 1 ,2 ,4
Let us test ....
P Q P/Q F(P/Q) Divisor
-1 1 -1.00 13.00
-1 3 -0.33 5.00
-1 9 -0.11 4.11
-2 1 -2.00 40.00
-2 3 -0.67 8.00
Note - For tidiness, printing of 13 checks which found no root was suppressed
Polynomial Roots Calculator found no rational roots
Final result :
45 • (9x2 + 4)