The volume of the shape is approximately 19130.95 cm³.
The volume of the shape shown in the diagram, we need to calculate the volume of the cylinder and the volume of the hemisphere separately, and then add them together.
Hight of cylinder = 23cm
Radius of hemisphere and cylinder = 11 cm
Step 1:-
The volume of the cylinder using the formula V = πr²h.
V cylinder = 3.14 × (11cm)² × 23 cm
V cylinder ≈ 8738.62 cm³.
Step 2 :-
V hemisphere =
 (
(
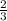 πr³ )
πr³ )
V hemisphere =
 × (
× (
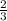 ×(3.14) ×
×(3.14) ×
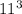 )
)
V hemisphere ≈ 1392.11 cm³.
Step 3 :-
Two volumes together to get the total volume: V total = V cylinder + V hemisphere
V total ≈ 8738.62 cm³ + 1392.11 cm³
V total ≈ 19130.95 cm³.
Therefore, the volume of the shape is approximately 19130.95 cm³.