Answer:
See below
Explanation:
the n number of value of x
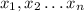
let it be
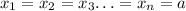
now, the A.M of x is
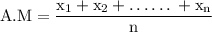
since every value equal to a
substitute:
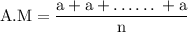
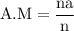
reduce fraction:
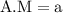
the G.M of x is
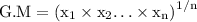
since every value equal to a
substitute:
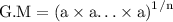
recall law of exponent:
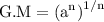
recall law of exponent:
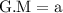
the H.M of x is
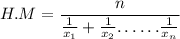
since every value equal to a
substitute:
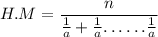
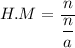
simplify complex fraction:
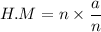
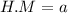
so
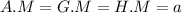
hence,