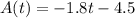Answer:
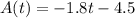
Explanation:
Mr.Mole's digging can be described by a linear model of general equation:
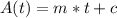
Where "m" is the rate at which he descends. Note that since the function A(t) measure his altitude relative to the ground, the rate "m" must be negative.
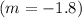
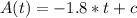
The constant "c" is his starting position. To find this value, assign the given data at t = 5 min to the equation above
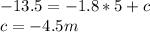
Therefore, the function A(t) is described by the following formula: