Question

The bearing of c from a is 210°

(i) find the bearing of B from A

(ii) find the bearing of A from B

if you could also solve the question above I'd be very grateful
I need it in at least 10 minutes so please answer it!! ♡♡​

Answer 1

(a) His speed when he runs from C to A is
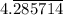`4.\overline {285714}` m/s

(i) The bearing of B from A is approximately 127.18°

(ii) The bearing of A from B is approximately 307.18°

Explanation:

(a) The given parameters are;

The distance from A to B = 120 m

The speed with which Olay runs from A to B, v₁ = 4 m/s

The distance from B to C = 180 m

The speed with which Olay runs from B to C, v₂ = 3 m/s

The distance from C to A = 150 m

His average speed for the whole journey = 3.6 m/s

We find

The total distance of running from A back to A, d = 120 m + 180 m + 150 m = 450 m

The time it takes to run from A to B, t₁ = 120 m/(4m/s) = 30 seconds

The time it takes to run from B to C, t₂ = 180 m/(3m/s) = 60 seconds

Let t₃ represent the time it takes Olay to run from C to A

We have;

The total time it takes to run from A back to A = t₁ + t₂ + t₃

Therefore;

`Average \ velocity = (Total \ distance )/(Total \ time) = (d)/(t_1 + t_2 + t_3)`

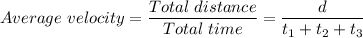
Substituting the known values for the average velocity, 'd', 't₁' and 't₂' gives;

`Average \ velocity = 3.6 \, m/s = (450 \, m)/(30 \, s + 60 \, s + t_3)`

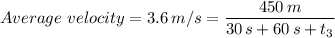
3.6 m/s × (30 s + 60 s + t₃) = 450 m

3.6 m/s × 30 s + 3.6 m/s × 60 s + 3.6 m/s × t₃ = 450 m

108 m + 216 m + 3.6 m/s × t₃ = 450 m

∴ 3.6 m/s × t₃ = 450 m - (108 m + 216 m) = 126 m

t₃ = 126 m/(3.6 m/s) = 35 s

The speed with which Olay runs from C to A, v₃ = Distance from C to A/t₃

The speed with which he runs from C to A = 150 m/(35 s) = 30/7 m/s =
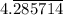`4.\overline {285714}` m/s

(i) The given bearing of C from A = 210°

By cosine rule, we have;

a² = b² + c² - 2·b·c·cos(A)

∴ cos(A) = (b² + c² - a²)/(2·b·c)

Where;

a = The distance from B to C = 180 m

b = The distance from C to A = 150 m

c = The distance from A to B = 120 m

We find;

cos(A) = (150² + 120² - 180²)/(2 × 150 × 120) = 0.125

A = arccos(0.125) ≈ 82.82°

The bearing of B from A ≈ 210° - 82.82° ≈ 127.18°

The bearing of B from A ≈ 127.18°

(ii) The angle, θ, formed by the path of the bearing of A from B is an alternate to the supplementary angle of the bearing of B from A

Therefore, we have;

θ ≈ 180°- 127.18° ≈ 52.82°

The bearing of A from B = The sum of angle at a point less θ

∴ The bearing of A from B = 360° - 52.82° ≈ 307.18°

The bearing of A from B ≈ 307.18°.