Answer:
The sum of the first 880 terms in the sequence is 2,273,920.
Explanation:
Arithmetic sequence:
The difference between consecutive terms is always the same, called common difference, and the nth term is given by:
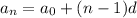
In which d is the common difference.
Sum of the first n terms:
The sum of the first n terms of an arithmetic sequence is given by:
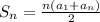
ai = ai-1 + 6
This means that

In this question:
Sum of the first 800 terms, so
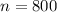
First term is -53, so
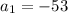
The 880th term is:

Sum
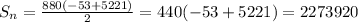
The sum of the first 880 terms in the sequence is 2,273,920.