Question

a glass bottle full of mercury has mass of 500g on being heated through 35 degree celsuis,2.43g of mercury are expelled .calculate the mass of the mercury remaining in the bottle​

Answer 1

The mass of the mercury remaining in the bottle is 497.57 grams.

Step-by-step explanation:

The mass of the mercury remaining in the bottle is found by subtracting the mass expeled due to heating from initial mass inside the bottle. That is:

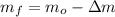`m_(f) = m_(o)-\Delta m` (1)

Where:

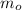`m_(o)` - Initial mass, in grams.

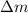`\Delta m` - Mass expelled due to heating, in grams.

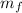`m_(f)` - Final mass, in grams.

If we know that
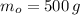`m_(o) = 500\,g` and
`\Delta m = 2.43\,g`, then the mass of the mercury remaining in the bottle is:

`m_(f) = m_(o)-\Delta m`

`m_(f) = 497.57\,g`

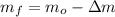
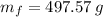
The mass of the mercury remaining in the bottle is 497.57 grams.