Question

PQ is a straight line segment.According to the information marked in the figure, (I) Find the magnitude of PÔS. (ii) Find magnitude of SÔQ.

PLEASEEEEEEE HEELPPP!!
99 POINTS!! btw turn the attached picture upside down​

Answer 1

magnitude of PÔS = 60°

magnitude of SÔQ = 120°

note: a straight line has always 180°

solve for x:

• PÔS + SÔQ = 180°

• 3x + 2x + 80° = 180°

• 5x = 180° - 80°

• 5x = 100°

• x = 20°

m∠POS

• 3x

• 3(20°)

• 60°

m∠SOQ

• 2x + 80°

• 2(20°) + 80°

• 40° + 80°

• 120°

Answer 2

So to find angle POS and SOQ we have to find value of x first.

`\\`

`\rm \angle POS + \angle SOR + \angle ROQ = 180 \degree \\`

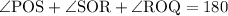
Reason:-

Sum of angles on same line.

By the way it can be any number of angles but they should meet at same point. And their sum is always 180°. Remember linear pair? It is also same aspect but there will be only two angles.

`\\`

So:-

`\\`

`\dashrightarrow \sf \angle POS + \angle SOR + \angle ROQ = 180 \degree \\`

`\\`

`\dashrightarrow \sf 3x + 2x+ 80= 180 \degree \\`

`\\`

`\dashrightarrow \sf 5x+ 80= 180 \degree \\`

`\\`

`\dashrightarrow \sf 5x= 180 - 80 \degree \\`

`\\`

`\dashrightarrow \sf 5x= 100 \degree \\`

`\\`

`\dashrightarrow \sf x= (100)/(5) \degree \\`

`\\`

`\dashrightarrow \sf x= (5 * 20)/(5) \degree \\`

`\\`

`\dashrightarrow \sf x= (\cancel5 * 20)/(\cancel5) \degree \\`

`\\`

`\dashrightarrow \sf x= (1 * 20)/(1) \degree \\`

`\\`

`\dashrightarrow \bf x=20\degree \\`

`\\ \\`

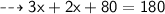
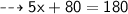
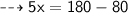
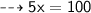
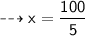
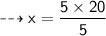
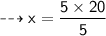
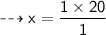
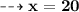
Verification:-

`\\`

`\dashrightarrow \sf 3x + 2x+ 80= 180 \degree \\`

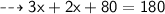
Put value of x

`\\`

`\dashrightarrow \sf( 3 * 20) + (2 * 20)+ 80= 180 \degree \\`

`\\`

`\dashrightarrow \sf60 + (2 * 20)+ 80= 180 \degree \\`

`\\`

`\dashrightarrow \sf60 + 40+ 80= 180 \degree \\`

`\\`

`\dashrightarrow \sf100+ 80= 180 \degree \\`

`\\`

`\dashrightarrow \bf180= 180 \degree \\`

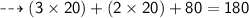
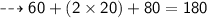
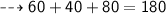
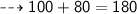
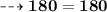
LHS = RHS

HENCE VERIFIED!

`\\`

• Angle POS = 3x
• Angle POS = 3 × 20
• Angle POS = 60°

• Angle SOQ = 2x + 80
• Angle ROQ = 2 × 20 + 80
• Angle ROQ = 40 + 80
• Angle ROQ = 120°