Question

The calibration of a scale is to be checked by weighing a 13 kg test specimen 25 times. Suppose that the results of different weighings are independent of one another and that the weight on each trial is normally distributed with Sigma = 0.200 kg. Let µ denote the true average weight reading on the scale.

Required:
a. What hypotheses should be tested?
b. With the sample mean itself as the test statistic, what is the P-value?

Answer 1

a).

Given : Number of times, n = 25

Sigma, σ = 0.200 kg

Weight, μ = 13 kg

Therefore the hypothesis should be tested are :

`$H_0 : \mu = 13 $`

`$H_a : \mu \\eq 13$`

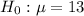
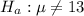
b). When the value of
`$\overline x = 12.84$`

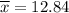
Test statics :

`$Z=((\overline x - \mu))/((\sigma)/(\sqrt n)) $`

`$Z=\frac{(14.82-13)}{\frac{0.2}{\sqrt {25}}} $`

`$=(1.82)/(0.04)$`

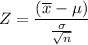
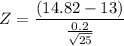
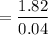
= 45.5

P-value = 2 x P(Z > 45.5)

= 2 x 1 -P (Z < 45.5) = 0

Reject the null hypothesis if P value < α = 0.01 level of significance.

So reject the null hypothesis.

Therefore, we conclude that the true mean measured weight differs from 13 kg.