Question

Calculate the value of (Ag+) in a saturated solution of AgCl in distilled water

Answer 1

`[Ag^+]=1.3x10^(-5)M`

Step-by-step explanation:

Hello there!

In this case, according to the dissociation of silver chloride in aqueous solution, we can write:

`AgCl(s)\rightarrow Ag^+(aq)+Cl^-(aq)`

Whereas the equilibrium expression is:

`Ksp=[Ag^+][Cl^-]`

And the solubility product constant is 1.7 x10⁻¹⁰; thus, by inserting x as the concentration of both silver and chloride ions as they are the same at equilibrium, we obtain:

`1.7x10^(-10)=x^2\\\\x=\sqrt{1.7x10^(-10)} \\x=1.3x10^(-5)M`

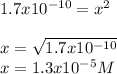
Which is also equal to the concentration silver ions at equilibrium in a saturated solution because we considered the Ksp.

`[Ag^+]=1.3x10^(-5)M`

Best regards!