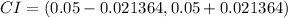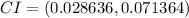Answer:
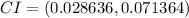
I am 95% confident that the true proportion of couples where the wife is taller than her husband is captured in the interval (.028, .071)
Explanation:
Given
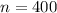
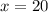 --- taller wife
--- taller wife
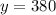 --- shorter wife
--- shorter wife
Required
Determine the 95% confidence interval of taller wives
First, calculate the proportion of taller wives
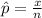
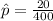
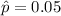
The z value for 95% confidence interval is:
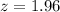
The confidence interval is calculated as:
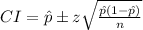
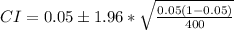
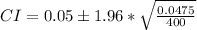
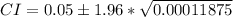

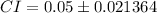
This gives: