Question

A student is asked to calculate the density of a small rock. An electronic scale

measures the mass of the rock as 12.1 grams. The student puts the rock in a large
graduated cylinder that is partially filled with water. The water level in the
graduated cylinder before the rock is added is 24.2 ml, and after the rock is added,
the level rises to 28.8 mL. What is the density of the rock, stated in grams per cubic
centimeter?

Answer 1

`\boxed {\boxed {\sf \rho \approx 2.63 \ g/cm^3}}`

Step-by-step explanation:

The density of an object is found by dividing the mass by the volume.

`\rho= \frac {m}{v}`

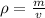
The mass is 12.1 grams, but we are not given the volume. Instead, we are told that the water before is 24.2 millilitres and the water after is 28.8 millilitres.

So, the volume was taken using water displacement. We can find the volume by subtracting the initial volume from the volume after the object was added.

• v= with object - initial
• v= 28.8 mL-24.2 mL=4.6 mL

Now we know the mass and volume:

`m= 12.1 \ g \\v= 4.6 \ mL`

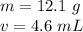
Substitute the values into the formula.

`\rho= \frac {12.1 \ g }{ 4.6 \ mL}`

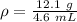
Divide.

`\rho= 2.63043478261 \ g/mL`

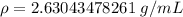
Let's round to the nearest hundredth. The 0 in the thousandth place tells us to leave the 3.

`\rho \approx 2.63 \ g/mL`

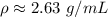
1 milliliter is equal to 1 cubic centimer, so the density can also be written as:

`\rho \approx 2.63 \ g/cm^3`

The density of the rock is approximately 2.63 grams per cubic centimeter.