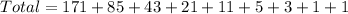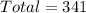Answer:
341 matches
Explanation:
Given
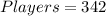

Required
Total number of matches.
The total number of matches is calculated by getting the number of matches in each round.
i.e.

So, we have:
Round 1
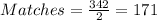
Round 2
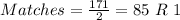 [R 1 means remainder 1]
[R 1 means remainder 1]
Round 3
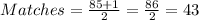
[The remainder is added to each round]
Round 4
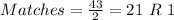
Round 5

Round 6

Round 7
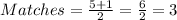
Round 8
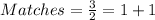
Round 9
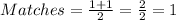
So, the total is: