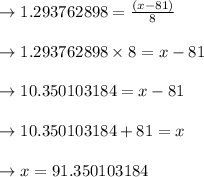Question

Pioneer company has given an aptitude test to 71 potential job applicants. The test score had an average of 81 and a standard deviation of 8. Aptitude tests are known to follow a t-distribution. Pioneer rejects the bottom 5% of the applicants right away. The top 5% are hired immediately at managerial positions.

A. What is the degrees of freedom for this distribution?
B. What is the t-score for someone who has scored 93?
C. What is the cutoff score for those who'll be hired as managers?
D. What will be the cutoff score fro those who'll get rejected right away?
E. If we want to define the middle of the class (80%) to be average, what will be the lower cut-off scores?
F. If we want to define the middle of the class (80%) to be average, what will be the upper cut-off scores?

Answer 1

Follows are the solution to the given points:

Explanation:

In point A:

`\to df = n - 1 = 71-1= 70`

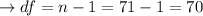
In point B:

`\to t = ((x -X))/(s) = ((93-81))/(8) = (12)/(8)= 1.5`

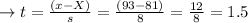
In point C:

For df = 70, the top 5% critical t score

tcrit = 1.666914479

Thus,

`\to 1.666914479 = ((x - 81))/(8)\\\\\to 1.666914479 * 8 = (x - 81)\\\\\to 13.335315832 = (x - 81)\\\\\to 13.335315832 +81 =x \\\\\to x= 94.335315832`

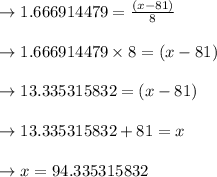
In point D:

For df = 70, the top 5% critical t score

tcrit = -1.666914479

`\to -1.666914479 = ((x - 81))/(8)\\\\\to -1.666914479 * 8= (x - 81)\\\\\to -13.335315832= (x - 81)\\\\\to -13.335315832+81 = x \\\\\to x = 67.664684168\\\\`

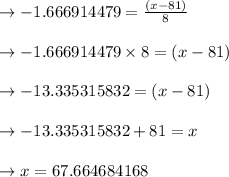
In point E:

The lower cutoff is 0.10 in the center, which would be around 80 %. The critical point therefore is

tcrit = -1.293762898

`\to -1.293762898 = ((x-81))/(8)\\\\\to -1.293762898 * 8= (x-81) \\\\\to -1.293762898 * 8= (x-81) \\\\\to -10.350103184=x-81\\\\\to -10.350103184+81=x\\\\\to x=70.649896816`

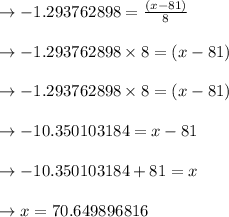
In point F:

The lower cutoff is 0.90 in the center, which would be around 80 %. The critical point therefore is

tcrit = 1.293762898

`\to 1.293762898 = ((x-81))/(8)\\\\\to 1.293762898 * 8= x-81\\\\\to 10.350103184 =x-81\\\\\to 10.350103184 +81=x\\\\\to x = 91.350103184\\`